DOI: 10.1016/j.jestch.2020.12.017
在此,研究者對靜電紡絲過程中聚合物溶液的單軸拉伸流動進行了數值模擬和實驗研究。數值模型的建立考慮了材料的粘彈性。因此,控制方程由有限可擴展的非線性彈性本構模型支持,并首次采用FENE-CR模型。這個版本的FENE模型可以很好地描述拉伸流動的流變性。為了對其進行驗證,使用聚酰胺6(PA6)聚合物溶液進行實驗研究。重點討論了最終纖維直徑的測定以及聚合物初始濃度對纖維直徑的影響。此外,還研究了不同濃度方案對減薄動力學的影響。數值模擬和實驗的比較結果充分證明了模擬的預測能力。這項研究所采用的數值方法不僅捕捉到材料的粘彈性行為,而且還觀測到由于溶劑蒸發而導致納米纖維的固化。由于靜電紡絲的定量預測模型尚不完善,本研究為模擬該工藝提供了很好的見解。
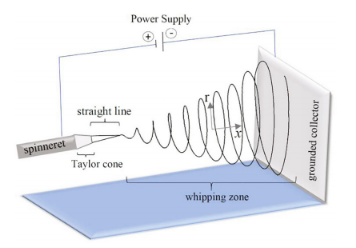
圖1.靜電紡絲裝置。
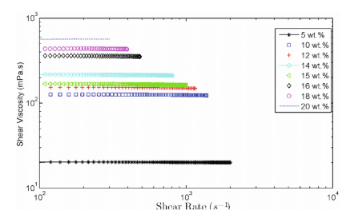
圖2.不同濃度下PA6溶液在FA中的剪切粘度變化。
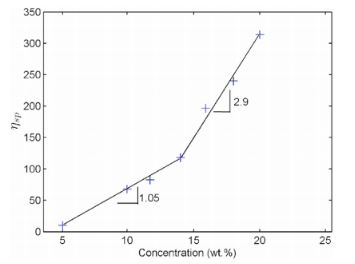
圖3.PA6在FA中比粘度的濃度依賴性。
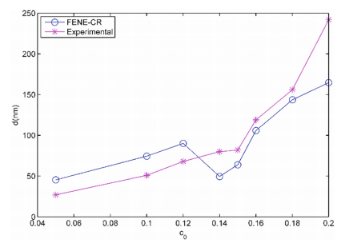
圖4.實驗和數值纖維直徑與初始聚合物溶液濃度c0之間的關系。

圖5.用5wt%-20wt%的不同濃度聚合物溶液制備纖維的SEM顯微照片。對于每種情況,提供了作為插圖的特寫圖片。
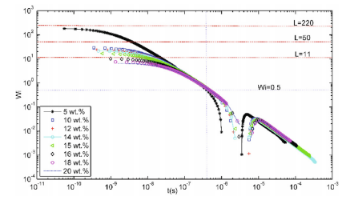
圖6.不同濃度溶液的魏森伯格數隨時間的變化。
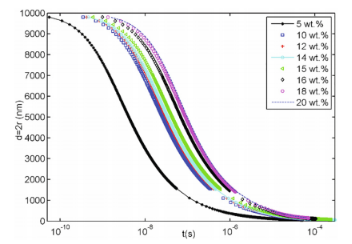
圖7.對于初始濃度c0在5wt%-20wt%之間的聚合物溶液,其纖維直徑d=2r隨時間的變化。
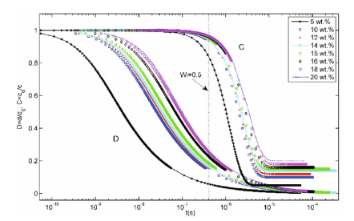
圖8.對于初始濃度c0在5wt%-20wt%之間的聚合物溶液,其無量綱化纖維直徑D=d/d0和無量綱化聚合物組分C=c0/c隨時間的變化。
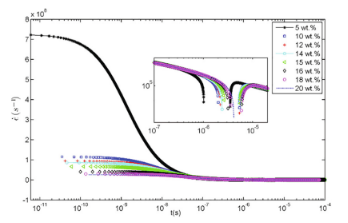
圖9.對于初始濃度c0在5wt%-20wt%之間的聚合物溶液,其應變速率隨時間的變化。插圖為顯示應變速率突然下降的log-log圖的特寫圖片。
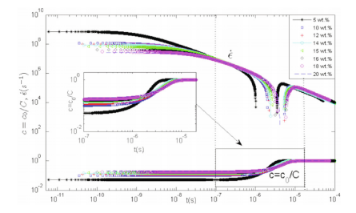
圖10.對于初始濃度c0在5wt%-20wt%之間的聚合物溶液,其應變速率和濃度隨時間變化的Log-Log圖。還給出了c在10-7s-10-5s時間范圍內的特寫圖像。
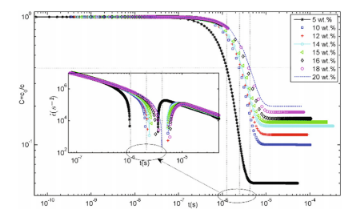
圖11.對于初始濃度c0在5wt%-20wt%之間的聚合物溶液,其無量綱化聚合物組分隨時間變化的Log-Log圖。插圖還給出了應變速率下降(log-log圖)的特寫圖像。
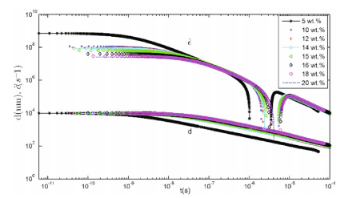
圖12.對于初始濃度c0在5wt%-20wt%之間的聚合物溶液,其應變速率和纖維直徑隨時間變化的Log-Log圖。
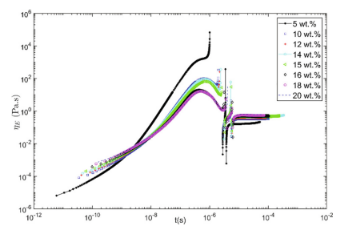
圖13.對于初始濃度c0在5wt%-20wt%之間的聚合物溶液,其ηE隨時間的變化。
 微信二維碼
微信二維碼