DOI:10.1016/j.jmbbm.2020.103634
本文僅以單纖維的幾何和彈塑性力學性能為基礎,輔以膜的重量和體積的測量,預測了電紡聚丙交酯膜的三維結構和宏觀力學響應,并將所得計算模型應用于電紡網絡的非仿射微運動學研究。為此,從膜的掃描電子顯微照片中提取描述面內纖維形態的統計參數,并通過匹配真實纖維墊的孔隙率來生成計算網絡模型。將虛擬網絡在結構上與計算機斷層掃描進行比較,并就其宏觀力學響應與單軸拉伸測試進行比較。所獲得的虛擬網絡結構與實際網絡中的纖維配置非常吻合,對平均直徑為1.10μm和0.70μm的兩種膜的力學響應的嚴格預測定性地捕獲了實驗行為。但是,只有在降低單纖維測試中確定的楊氏模量,屈服應力和硬化斜率,并在纖維較細的膜模型中降低纖維間鍵的密度后,才能獲得良好的定量一致性。模擬結果證明了研究電紡網絡多尺度力學方法的有效性和優點,但也指出了網絡中電紡纖維的特性與為單纖維表征而產生的性能之間的潛在差異,并突顯了電紡網絡中纖維之間鍵合密度和質量的現有不確定性。

圖1.(a)樣品電紡材料的閾值CT。(b)從CT數據的后處理中提取的纖維中心線。(c)從微觀結構已知的數值模型中提取的纖維中心線。
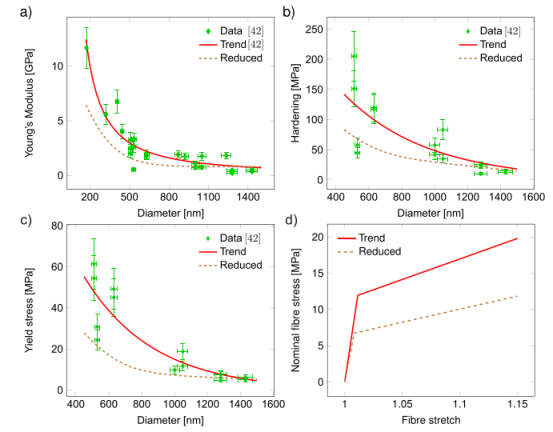
圖2.取決于纖維直徑的單纖維材料參數。具有合適的擬合趨勢線和減小關系的(a)楊氏模量、(b)硬化和(c)屈服應力的實驗數據。(c)比較具有擬合趨勢的直徑dF=1.10和參數減小的纖維的單纖維標稱應力-拉伸曲線。
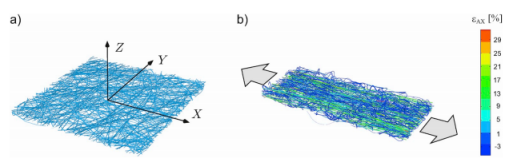
圖3.單軸載荷下離散網絡的有限元模擬。(a)參考配置。(b)模型對施加的縱向網絡拉伸(λx=1.15)的典型響應,顯示局部軸向基本應變εAX。
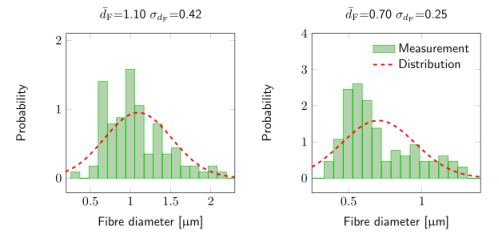
圖4.(a)樣品I和(b)樣品II的單纖維直徑和相應的高斯分布直方圖。

圖5.(a,b)樣品I和(b,d)樣品II離散模型的(a,b)SEM和(c,d)渲染圖像的俯視分解圖。比例尺適用于所有圖像。
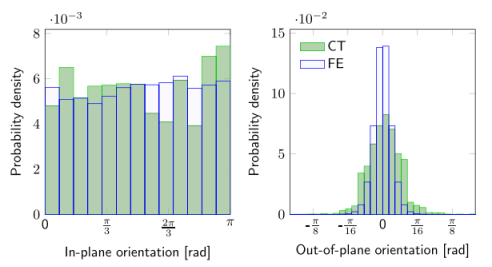
圖6.從微結構信息有限元模型和電紡樣品的CT中獲得的面內和面外定向分布比較。
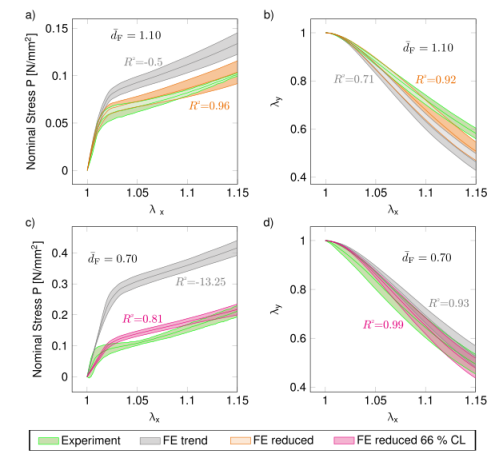
圖7.(a)實驗獲得的樣品I和(c)樣品II的數值模型和通過數值模型預測的應力-拉伸曲線的比較,以及(b)樣品I和(d)樣品II的面內橫向拉伸與縱向拉伸λy-λx曲線。所有圖表分別顯示N=3個數據集的平均值和標準偏差(陰影區域)。用各自的平均值評估確定系數。
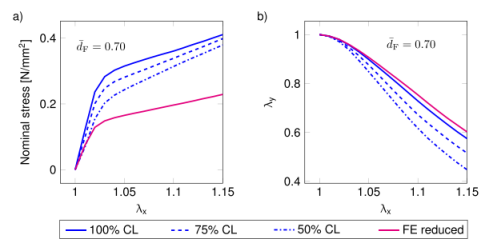
圖8.(a)交聯量和減少的材料參數對數值模型預測的應力-拉伸曲線的影響,以及(b)樣品II的面內橫向與縱向拉伸λx-λy曲線的影響。
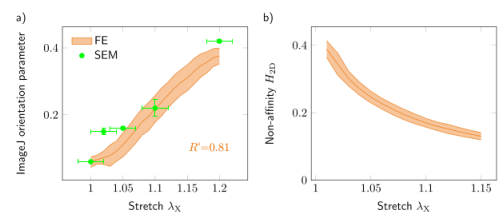
圖9.(a)由ImageJ定向參數量化的纖維重新定向的比較,該參數來自后處理的俯視SEM和離散模型的渲染圖像。對于SEM數據,假定網絡拉伸λ1的誤差為2%。(b)由參數H2D(等式(8))定量的單軸張力中的非仿射變形,該參數由具有降低單纖維性能的樣品I的數據模型顯示。SEM數據的ImageJ定向參數的誤差以及FE數據的陰影區域分別代表N=3個數據集的標準偏差。(a)中的測定系數用各自的平均值評估。
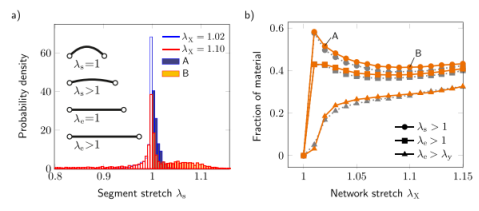
圖10.(a)兩個宏觀網絡拉伸λx的纖維拉伸分布直方圖。直方圖的藍色和橙色陰影部分分別表示A:λx=1.02和B:λx=1.10的細長段(λs>1)的片段。(b)具有細長纖維段(λs,λe> 1)或段拉伸超過其屈服閾值(λe>λy)的纖維材料的片段。樣品I的數值模型給出的數據具有減少的材料(橙色實線)和初步確定的(虛線灰色)性能(見圖2b)。
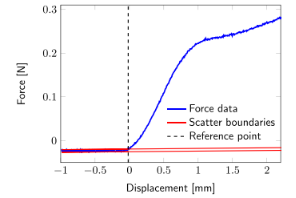
圖A1.參考點算法用于力-位移數據。紅線顯示分散邊界。黑色虛線表示定義的參考點。
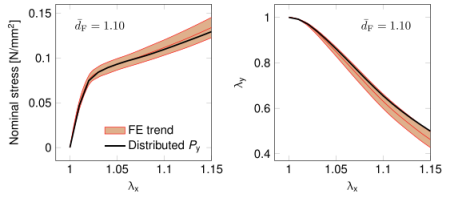
圖B2.樣本I的微結構離散模型對單軸張力的響應的比較(通過擬合的單纖維機械參數的平均值(FE趨勢)與正態分布的單纖維屈服應力(分布式Py)進行比較)。FE趨勢的值表示為平均值和標準偏差(陰影區域)。
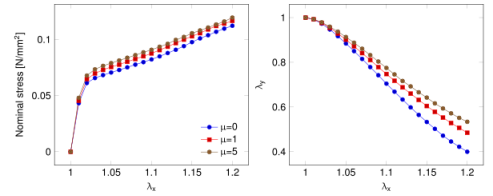
圖C3.摩擦系數μ對樣品I網絡模型的宏觀響應的影響。
 微信二維碼
微信二維碼